A trapezoid is a quadrilateral that has one pair of parallel sides. The only sufficient condition for a quadrilateral to be a trapezoid is that it has only one pair of parallel sides.
Perimeter
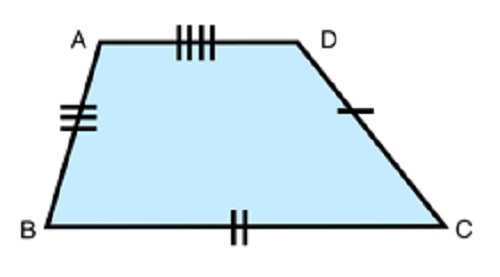
Labels on the sides of this geometric 2D figure are:
- The longer side of the pair of parallel sides is denoted by a.
- The shorter side of the pair of parallel sides is denoted by b.
- The sides that are not parallel are indicated by c and d.
The perimeter of is calculated using the formula:
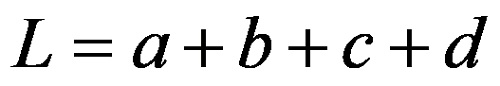
Example number 1: Calculate the perimeter of a trapezoid whose bases are 15cm and 11cm, if the pair of sides that are not parallel have lengths of 4cm and 4.5cm.
To determine the perimeter of the trapezoid from example 1, it is enough to calculate the sum of all its sides: L=15cm+11cm+4.5cm+4cm
The perimeter of this geometric figure is 34.5 cm.
Area of a trapezoid
The formula for determining the area of a trapezoid is:
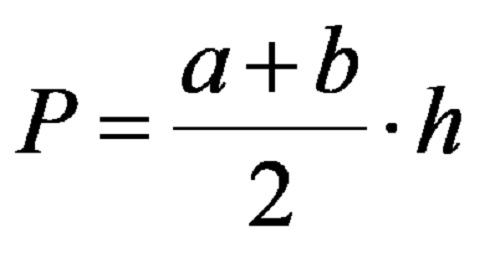
In the formula, the symbol h is in use for the height of the trapezoid.
Example number 2: Calculate the area of a trapezoid with bases 12cm and 8cm, if its height is 6cm.
The calculation for determining the area can proceed as follows:
- The sum a+b is: 12cm + 8cm = 20cm
- Then the sum of a+b in division by 2: 20cm : 2 = 10cm
- The result of step 2 is in multiplication by the height.
Finally, the area of the figure from example number two is 60 square centimeters.
Isosceles trapezoid
Isosceles is the trapezoid in which the length of the pair of non-parallel sides is equal, that is, the length of sides c and d is equal. Due to the equality of the two non-parallel sides, both are c.
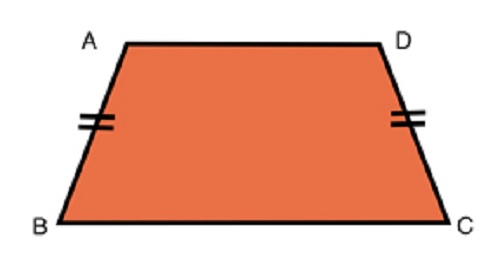
The formulas for calculating the perimeter and area in this variant are identical to the formulas above that apply to any other member of this figure.
A rectangular trapezoid
A trapezoid is rectangular, which has exactly two right angles of 90 degrees each.
The formula for calculating the area of the rectangular variant remains in the same form as for the perimeter of any other member of this geometric figure.
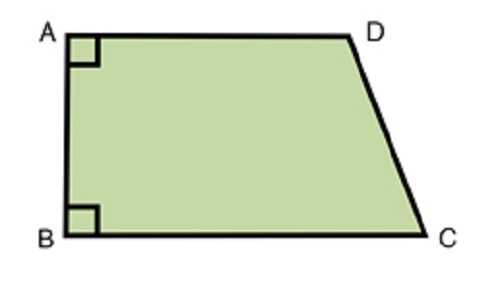
The formula for area takes the following variant:
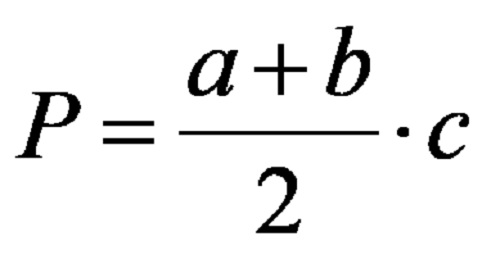
In the last formula, unlike the general formula for the area of this geometric figure, we can replace the height h with the length of the side c (the side on which they lie, i.e. the two right angles belong).
Example number 3: Calculate the area of a trapezoid with bases 15cm and 13cm, if its side c, which forms a right angle with the bases, is 8cm.
The calculation for determining the area of a rectangular trapezoid can proceed as follows:
- The sum a+b is: 15cm + 13cm = 28cm
- Then the sum of a+b in division by 2: 28cm : 2 = 14cm
- The result of step 2 is in multiplication by the length of side c.
Finally, the area of the figure from example number three is 112 square centimeters.
In the end, every trapezoid has two diagonals that are equal in length only in the isosceles. Only the isosceles have one axis of symmetry, while any other (other than the isosceles) has no axis of symmetry.
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Area, Formula, Isosceles trapezoid, Perimeter, Rectangular trapezoid, Trapezoid, Trapezoids, Types

 Please wait...
Please wait...

