How can the total electrical resistance in a parallel circuit be calculated? Below, you can see examples of a parallel current circuit containing three parallel connected consumers with different electrical resistance. For this circuit, you can see the calculation of its total resistance. This calculation is on a page using a formula for calculating total resistance.
The formula for total resistance in a parallel circuit
Calculating total electrical resistance in a parallel circuit is more complicated than calculating total electrical resistance in a series circuit! The formula (in case there are three consumers (resistors) in the parallel circuit) is:
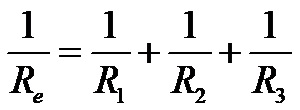
If the circuit has more than three consumers, then in the formula we just add their reciprocal values as a new addition in the sequence that follows.
It is seen from the formula that the reciprocal value of the total (equivalent) electrical resistance in parallel connection is the sum of the reciprocal values of the individual electrical resistances that the circuit contains.
To solve a problem of this type you must know all about adding fractions!
An example of total resistance in a parallel circuit
Below you have a fully solved example! It determines the total electrical resistance in a circuit containing only parallel connected consumers!
Example 1: Calculate the total (equivalent) electrical resistance of the circuit shown in the image below!
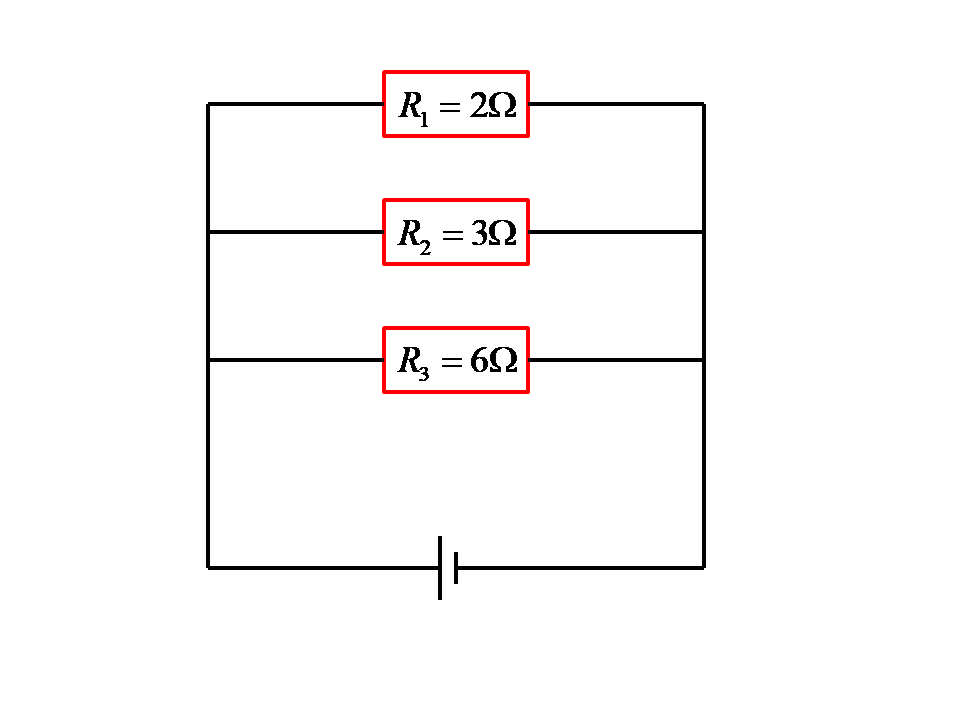
From the figure above we see that the electrical resistances of the consumers in the circuit are 2.3 and 6 ohms. By substituting these values in the formula for calculating total electrical resistance for a parallel current circuit, the following expression is:
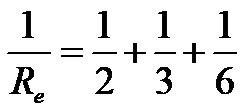
The numbers 2, 3, and 6 are the denominators of the various fractions in the expression above. To add these fractions we first need to determine the LCM of the numbers 2,3 and 6! Knowing that the smallest common denominator for the numbers 2,3 and 6 is the number 6, we expand all three fractions to the fraction that contains the number 6 in the denominator. The expression after expansion looks like this:
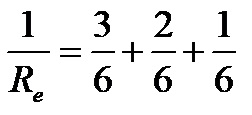
Now that all the fractions have the same denominator, we can easily add them, which gives us the next step:
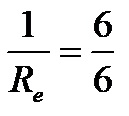
Finally, although the expression can be solved in several ways (by proportion, cross multiplication, etc.), to get only the total resistance on the left side instead of the reciprocal value of the total resistance, it is enough to turn the fractions on both sides upside down in the direction numerator-denominator. This gives you the solution itself:
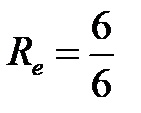
It is already clear that the total electrical resistance for the circuit of example 1 is 1 ohm!
Video examples
The video below contains an example of total electrical resistance in a parallel circuit!
Also, follow the information and materials that will be deliver in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Circuit, Examples, Formula, Parallel, Resistance, Total


 Please wait...
Please wait...

