Which method should be used for simplifying fractions to their simplest form? Below, you have a rule for simplifying fractions and two different approaches to simplifying (shortening).
Rule for simplifying fractions
To write a certain fraction in the correct form (irreducible fraction), we need to convert it to its simplest form. For a fraction to be in its simplest form, its numerator, and denominator should be two numbers that have no common divisor other than the number 1!
The rule that can help us in one step to perform the necessary conversion to the simplest form of the fraction reads:
- First, we determine the greatest common divisor of the numerator and denominator.
- We divide the numerator and the denominator by the number that is their greatest common divisor.
If we carry out the two steps described above in the correct way, then the fraction that we will get after simplifying is in its simplest form.
An example of using the rule
Example 1: Simplify the given fraction below to its simplest form!
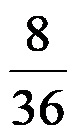
First method!
If we use the above rule for simplifying fractions it follows that we first need to determine the greatest divisor for the numerator and denominator (remember how to do this)!
GCD (8.36) = 4
The largest divisor (a number by which we can divide both the numerator and the denominator, which is the largest of all such possible numbers) for the numbers 8 and 36 is the number 4. After dividing the numerator and the denominator, simultaneously, with the number 4, the following result is obtained :
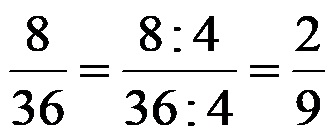
We conclude that the fraction 2/9 is the simplest form of the fraction 8/36!
Second method!
We can simplify the fraction 8/36 in two steps. If you don’t want to look for the greatest common divisor of the numerator and denominator, you don’t have to. For example, we can start with the fact that 8 and 36 are even numbers. As soon as they are even, it means that they are surely divisible by the number 2. It is correct if we decide to shorten the fraction 8/36 by the number 2. After dividing the by the number 2, the following entry for the same initial fraction is simultaneously obtained:
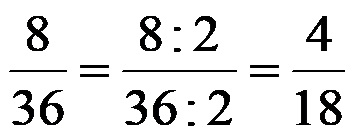
The resulting result, ie the fraction 4/18 is just another entry for the equivalent fraction of the fraction 8/36. For this new entry (because 4 and 18 are even numbers), we can further divide it by the number 2. If we carry this out a second time, we get the following solution:
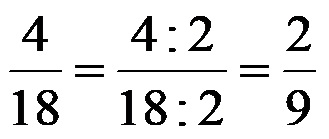
As can be easily observed, the solution obtained by the first methodology and the solution obtained by the second methodology are the same. This shows that no matter how we simplify fractions (whether using GCD or not), if we simplify correctly, we will always end up with the correct simplest representation of the fraction we are shortening!
Video examples
The video below contains examples of simplifying fractions to their simplest form, using the first method using the greatest common divisor!
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Divisor, Form, Fractions, Shortening, Simplest, Simplify, Simplifying


 Please wait...
Please wait...

