A rhomboid is a quadrilateral that has:
- Two by two parallel opposite sides
- Two by two equal opposite sides
- Two by two equal opposite angles
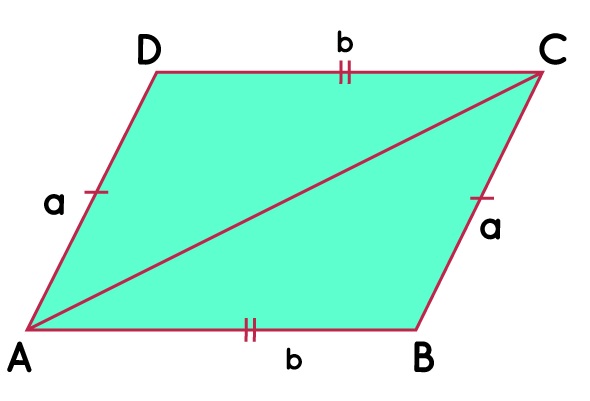
A rhomboid differs from a rhombus due to the length of its sides, while it differs from a rectangle due to the size of its angles.
Perimeter
The formula for calculating the perimeter of this 2D shape is:
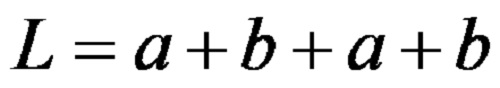
The same formula written using multiples in a shorter form is:
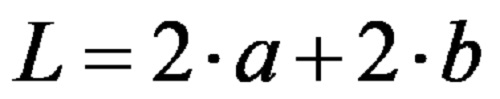
Example number one: Find the perimeter of a rhomboid if the length of its longer side is 10cm and the length of its shorter side is 7cm.
To solve the task from example number one, it is enough to:
a) Calculate the sum of the lengths of all four sides. The measurements are: in two places the longer side and in two places the shorter side: L=10cm+7cm+10cm+7cm
b) To calculate a sum of two different doublings of the values of the longer and shorter sides.
The perimeter is 16 centimeters!
Area of a rhomboid
The formula for calculating the area of a rhomboid is:

The area of a rhomboid is available as the product of one of the sides and its corresponding height.
Example number two: Calculate the area of a rhomboid with a side of 7cm, if the length of its height (corresponding to the given side) is 5cm.
In the calculation, it is enough to multiply 7cm by 5cm.
The area from example number two is 35 square centimeters.
Formulas for calculating the perimeter and area of a rhomboid are an integral part of tasks in which the perimeter and area of complex figures are available. Also, the formulas are used as part of a task to calculate the area of certain geometric bodies. Bodies that have a side or more sides that have the shape of a rhomboid.
A rhomboid has two diagonals that are not of equal length. The two diagonals are cut exactly in half and form two equal angles. This geometric figure has no axis of symmetry.
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.

 Please wait...
Please wait...

