How to calculate the total electrical resistance in a series circuit? This page describes how to calculate the total resistance in a circuit. This method is only valid for a circuit that contains only series-connected consumers (resistors). In addition to the calculation formula, the page contains examples in different formats.
How to recognize a circuit in which consumers are in series? Simply, if the “plus” of the source of electric current is in connection to the “first” consumer, the first to the second, the second to the third, etc., and finally the last consumer to its “minus”. So all consumers are in series along a single conductor.
The formula for total electrical resistance in a series circuit
The formula for calculating the equivalent (total) electrical resistance in a circuit with series-connected consumers is:
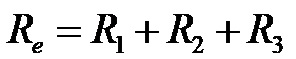
The total electrical resistance in this type of connection is calculated through the sum of all the individual resistances that exist in the circuit itself. The formula contains as many members as there are different consumers (resistors) in the circuit whose electrical resistance we are currently calculating! This formula is the for all difficult current circuits too, where there is any form of serial connection between consumers or groups of consumers.
Example 1: Calculate the total electrical resistance in the circuit shown in the figure below!
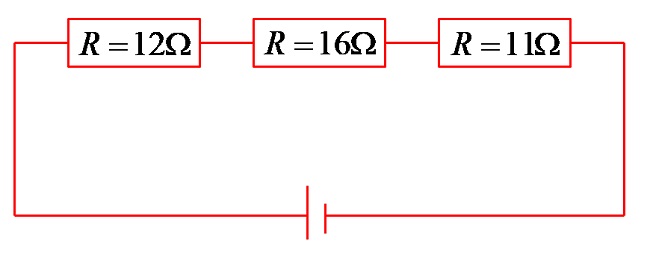
Obviously, the circuit contains three different consumers. By substituting the values for the electrical resistance of the different consumers, the expression is:
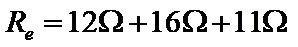
So after calculating the sum of the different resistances, the value for the equivalent electrical resistance is:
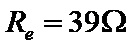
The short video below contains another example of calculating total resistance in a circuit with a series connection of consumers (resistors):
Finally, the formula is only valid for series-connected consumers (resistors) in a current circuit or combined current circuits in those parts where there is a series connection!
Also, follow the information and materials that will be deliver in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.


 Please wait...
Please wait...

