What is that quadrilateral that has no parallel sides? A quadrilateral without parallel sides may or may not have two or three equal sides.
Perimeter
The formula for calculating the perimeter of this geometric figure is:
Assuming that all four sides of the quadrilateral are of different lengths, their labels are: a, b, c and d. The sum of the four sides gives us the value for its perimeter.
Example number 1: Calculate the perimeter of a quadrilateral with side lengths of 5cm, 7cm, 3cm and 8cm.
To determine the perimeter of this quadrilateral, it is sufficient to calculate the sum of all four sides: L= 5cm + 7cm + 3cm +8cm.
The perimeter of this quadrilateral is 23 cm.
Area of a quadrilateral without parallel sides
The area of a quadrilateral without parallel sides can only be determined if one of its two diagonals is known. In that situation the quadrilateral is divided into two triangles. In doing so, the area of the triangles is calculated, so that finally their sum gives us the area of the quadrilateral itself.
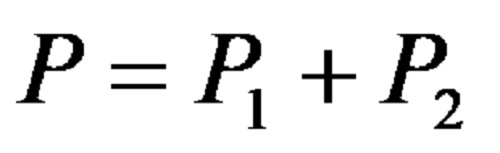
Example number 2: To determine the area of the quadrilateral shown in the figure below:
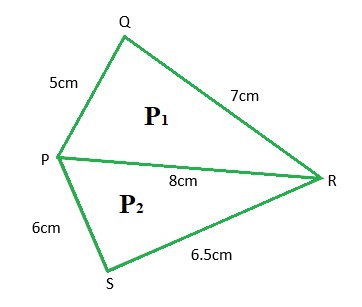
Obviously, the quadrilateral in the figure is combination of two triangles PRQ and PRS. To solve the problem, it is necessary to determine the area of the two triangles. Finally, the sum of the areas of the triangles represents the area of the quadrilateral.
The area of triangles in this situation can be calculated using Heron’s formula:
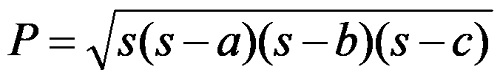
In the formula, s denotes half of the perimeter of the triangle, and the symbols a, b and c are the sides of the triangle.
The whole calculation has the following flow:
- Calculation of half the perimeter of the PRQ.
- Area of PRQ.
- Calculation of half the perimeter of the PRS.
- Area of PRS
- Sum of the areas PRQ and PRS.
Part One: Half Perimeter Calculation for Triangle PRQ:
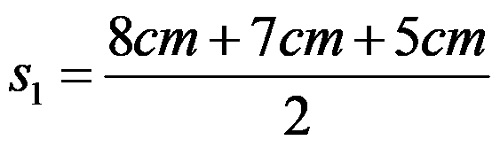
The length of the semi-perimeter of the triangle PRQ is 10 cm.
Second part: Calculation of the area of the triangle PRQ:
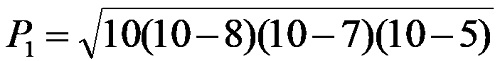
from which it follows that:
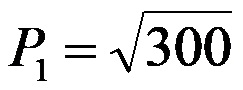
The area of triangle PRQ is approximately 17.32 square centimeters.
Part Three
Part Three: Half Perimeter Calculation for Triangle PRS:
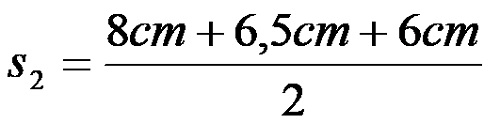
The length of the semi-perimeter of the triangle PRS is 10.25 cm.
Part Four: Calculation of the area of the triangle PRS:
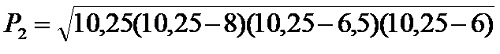
from which it follows that:
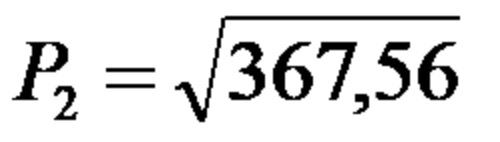
The area of triangle PRS is approximately 19.17 square centimeters.
Fifth part: Calculation of the sum of the areas of PRQ and PRS.
The area of the quadrilateral without parallel sides is approximately 36.49 square centimeters.
If a quadrilateral (without parallel sides) has two adjacent equal sides, it is a deltoid.
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Area, Formula, Heron's formula, Parallel, Perimeter, Quadrilateral, Sides, Without

 Please wait...
Please wait...

