Prime factor decomposition is a procedure in which a certain complex number is represented as a product of factors that are prime numbers!
As a reminder:
- A prime number is a number that is divisible by itself and the number 1. When dividing a prime number by any other number (different from 1 and from the number itself), a remainder is obtained.
- A complex number is any number which, in addition to being divisible by itself and the number 1, is divisible by at least one other number.
Data for prime factor decomposition
Below you can see three different examples of factoring prime factors with solution and explanation. Below these three examples you have a table that presents the decomposition of prime factors for the numbers from 1 to 100. In the table as data you can see all the prime numbers that exist in the range of numbers from 1 to 100. At the bottom of the page you video breakdowns of all numbers from 1 to 100 are available!
Examples of prime factor decomposition
Example 1: Break down the number 14 into prime factors!
We can represent the number 14 as a product of the numbers 2 and 7. Because both the number 2 and the number 7 are prime numbers, here the decomposition ends immediately after the first step is realized! On a drawing, we can present the solution in this way:
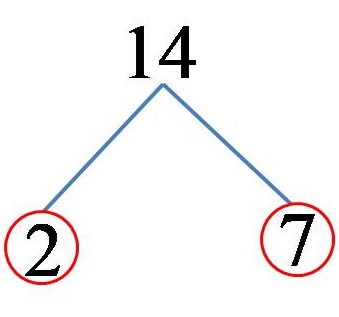
From which it follows that the number 14 decomposed into its prime multiples looks like this:
14 = 2 x 7
Example 2: Break down the number 30 into prime factors!
The number 30 can be represented as the product of the numbers 2 and 15. Because the number 2 is also a prime number, we have already obtained a prime factor for the number 30. On the other hand, the number 15 can be represented as the product of the numbers 3 and 5. The numbers 3 and 5 (both) are prime numbers, after which we conclude that the prime multiples of the number 30 are the numbers 2, 3 and 5. On a drawing, we can represent the solution in this way:
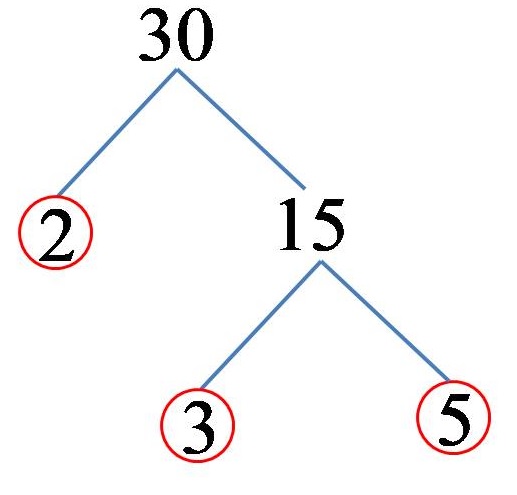
From which it follows that the number 30 decomposed into its prime multiples looks like this:
30 = 2 x 3 x 5
Example 3: Break down the number 42 into prime factors!
We can represent the number 42 as a product of the numbers 2 and 21. The number 2 is one of the prime multiples of the number 42! On the other hand, we can represent the number 21 as a product of the numbers 3 and 7. The numbers 3 and 7 (both) are prime numbers, after which we conclude that the prime multiples of the number 42 are the numbers 2,3 and 7. In the drawing, the solution we can represent it in this way:
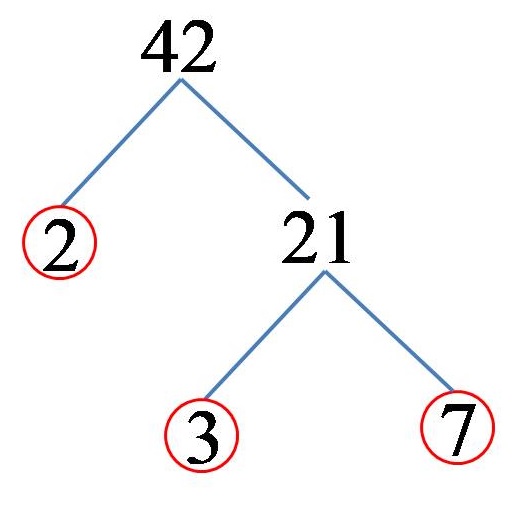
From which it follows that the number 42 decomposed into its prime multiples looks like this:
42 = 2 x 3 x 7
Table for decomposition
The table below contains information about the prime factorization of all numbers from 1 to 100, as well as data for all prime numbers that exist from 1 to 100!
| Number | Decomposition (if it’s possible) |
|---|---|
| 1 | Prime number |
| 2 | Prime number |
| 3 | Prime number |
| 4 | 4 = 2 x 2 |
| 5 | Prime number |
| 6 | 6 = 2 x 3 |
| 7 | Prime number |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Prime number |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Prime number |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Prime number |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Prime number |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Prime number |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Prime number |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Prime number |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Prime number |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Prime number |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Prime number |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Prime number |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Prime number |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Prime number |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Prime number |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Prime number |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Prime number |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Prime number |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Prime number |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Prime number |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Prime number |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Prime number |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Prime number |
Video examples
The video materials contain a step-by-step solution to factoring prime factors for all numbers from 1 to 100:
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: 1 to 100, Complex, Decomposition, Factor, Prime


 Please wait...
Please wait...

