On this page, you can see the rules for multiplication and division of fractions. Here you will meet only multiplication and division of fractions by fractions! On the page below you can see solved examples directly on the page itself and many solved examples in video format. Compared to addition and subtraction of fractions, multiplication, and division with fractions are much easier mathematical operations.
Multiplication of fractions
When multiplying fractions with fractions, the following rules apply:
- We get the numerator of the product of two fractions as a product of the numerators of the individual multiples (the individual fractions).
- We get the denominator of the product of two fractions as the product of the denominators, not the individual multiples (the individual fractions).
Example no. 1: Calculate the product of the fractions:
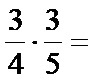
When multiplying the fractions from the example above, we calculate as follows:
a) We calculate the numerator of the product as a product of the numerator of the first fraction (the number 3) and the numerator of the second fraction (the number 3). The numerator of the product is 9!
b) We calculate the denominator of the product as a product of the denominator of the first fraction (the number 4) and the denominator of the second fraction (the number 5). The denominator of the product is 20!
You can see the entire resolution procedure below:
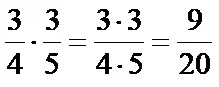
See more examples of multiplying fractions in the video below:
Division of fractions
When dividing fractions by fractions, the following rules apply:
- We rewrite the first fraction.
- We replace the division operation with multiplication.
- We “turn” the second fraction (the fraction by which we divide) upside down, that is, we write down the reciprocal value of the original fraction.
- Finally, we respect the rules when multiplying fractions!
Example no. 2: Calculate the quotient of the fractions:
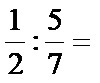
We start with the first three steps of the rules listed above. First, we rewrite the first fraction, then we change division by multiplication and write down the reciprocal of the second fraction. With that, we transform the expression given above into the following form:
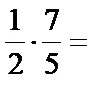
Then we follow the rules for multiplying fractions by fractions, which we already used when solving example number one. By applying them, the calculation of example number two is completed. The whole calculation looks like this:
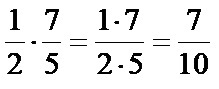
The video below contains more examples of dividing fractions:
It is easy to understand from the examples that multiplication and division of fractions are related operations. To divide fractions by fractions you first need to know how to multiply fractions by fractions!
Follow the information and materials that will be published in the future by connecting the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Division, Fractions, Multiplication



 Please wait...
Please wait...

