A kite is a trapezoid that has two adjacent equal sides. A kite is completely determined if the lengths of its unequal sides and the angle between them are known.
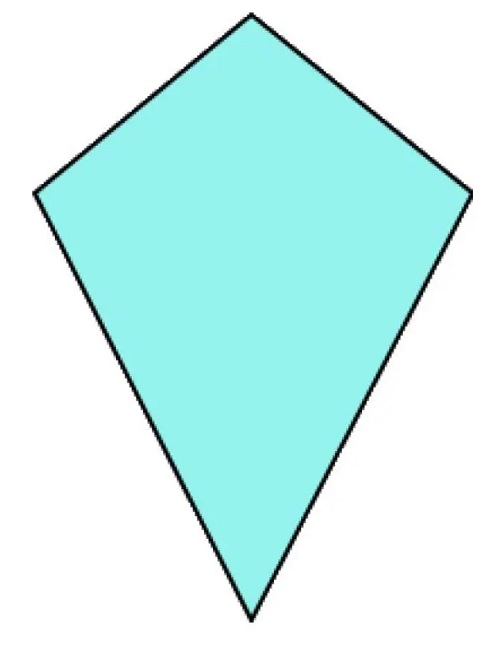
Perimeter
The formula for the perimeter is:
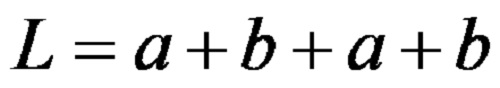
The same formula written using multiples in a shorter form is:
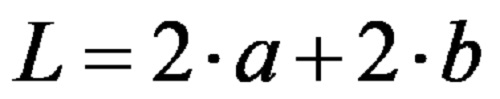
Example number 1. Calculate the perimeter of a kite if the length of its longer side is 15cm and the length of its shorter side is 11cm.
To solve the task from example number one, it is enough to:
a) Calculate the sum of the lengths of all four sides. The measurements are: in two places the longer side and in two places the shorter side: L=15cm+11cm+15cm+11cm
b) To calculate a sum of two different doublings of the values of the longer and shorter sides of the kite.
The perimeter is 52 centimeters!
Kite area
We can calculate the area of the kite using the Heron formula as with any other quadrilateral without parallel sides (see example solved problem by clicking on the link). The only difference is that the area of this 2D figure with Heron’s formula where the longer diagonal is known is easier to calculate because in that situation the kite is a combination of two identical triangles.
In addition to the standard solution method, the area is available using the formula:
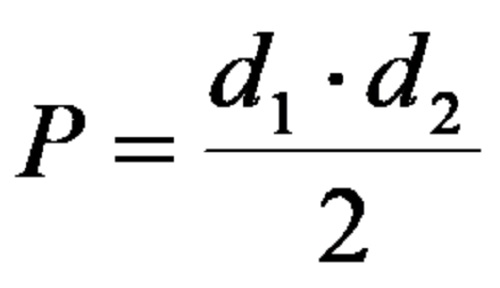
Of course, to use the formula directly, the length of the two diagonals needs to be available. If their length is available, the area can be easily available.
Example number 2: Calculate the area of a kite if the lengths of its diagonals are 3 cm and 16 cm.
To determine the area, it is enough:
- To determine the product of the diagonals.
- Divide the product of the diagonals by 2.
The area from example number two is 24 square centimeters.
The diagonals of this 2D shape always have different lengths. They intersect each other at a right angle (90-degree angle). The kite has one axis of symmetry.
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.

 Please wait...
Please wait...

