How can you learn how to simplify fractions before multiplying them? On this page you will see how to simplify fractions before multiplying them, thus avoiding the procedure of simplifying them after obtaining the final product. This method is easier because, at the moment before multiplication, it is easier to see which specific number can be simplified. After all, the numbers we are working with are still relatively smaller here.
Simplifying fractions before multiplication
When multiplying two fractions, you can simplify as follows:
We locate the numbers that, when the fractions are placed for multiplication, build an imaginary “diagonal”. Such two diagonals build:
- The numerator of the first fraction and the denominator of the second fraction
- The denominator of the first fraction and the denominator of the second fraction
Below, the two different imaginary diagonals are marked in the image with different colors!
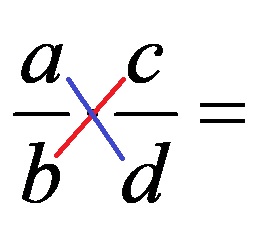
If the numbers that make up the diagonal have a greatest common divisor that is different from 1, then we divide both numbers by their GCM and write the quotient in their place. In this way, we can simplify only one or both diagonals!
Below, you can see examples where the simplification is done before we multiply the fractions together!
Examples
The first example below contains a simplification that is only possible along one diagonal, while the second example can be simplified along both diagonals!
Example 1: Simplify the fractions given below before doing the multiplication!
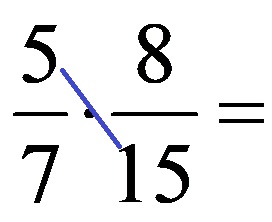
The GCM for the numbers located in the marked diagonal (numbers 5 and 15) is the number 5! Therefore, we divide both numbers by the number 5. The simplification should look like this:
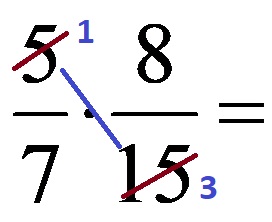
If we write the last expression without corrected numbers, it looks like this:
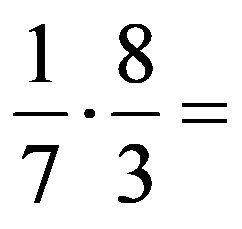
Finally, it remains to multiply the fractions, which gives the following final result:
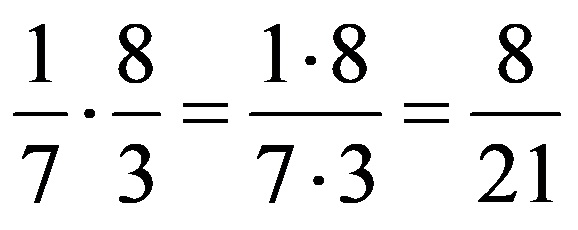
Example 2: Simplify fractions before multiplying them!
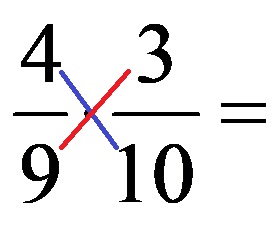
The GCM for the numbers in the blue diagonal (numbers 4 and 10) is the number 2! That’s why we divide both numbers by the number 2. On the other hand, the GCM for the numbers that are in the red diagonal (numbers 9 and 3) is the number 3. We divide the two numbers from the red diagonal by the number 3! After simplification, the following expression is obtained:
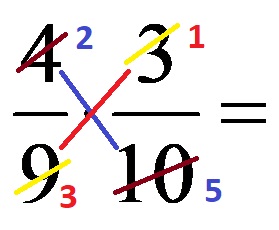
If we write the last expression without corrected numbers, it looks like this:
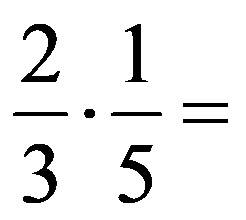
Finally, it remains to multiply the fractions, which gives the following final result:
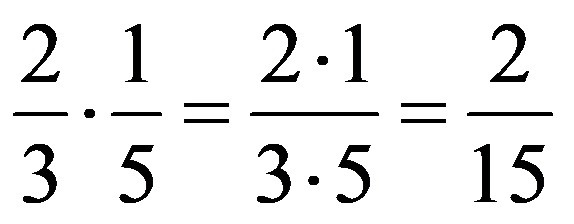
Video examples
In the video below you can see many examples of simplifying fractions before multiplying them together!
If, when multiplying fractions with each other, you decide not to practice simplifying them before multiplying them, then in the end (when you get their product), you must simplify the final result, which will most likely be in the form of a fraction!
Follow the information and materials that will be published in the future. Complete connection with the www.matematikazasite.com/en profiles on Facebook, and Youtube using the buttons below.
Tags: Before, Fraction, Fractions, How to simplify, Multiplying


 Please wait...
Please wait...

