Делтоид е трапезоид кој има две по две соседни еднакви страни. За еден делтоид може да се рече дека е целосно определен ако се познати должините на неговите нееднакви страни и аголот помеѓу нив.
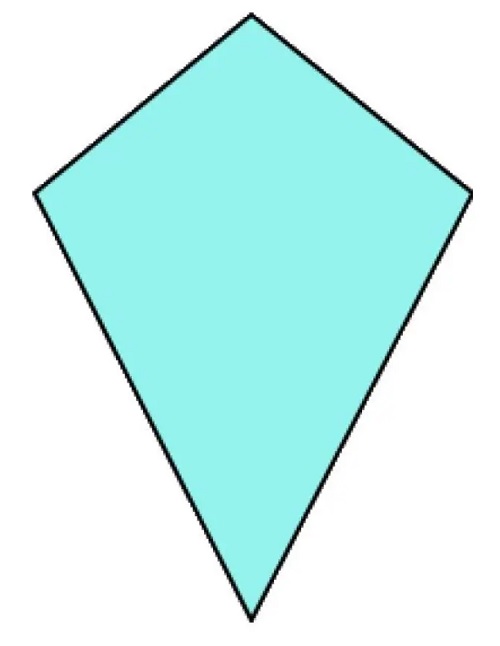
Периметар
Формулата за периметар на делтоид гласи:
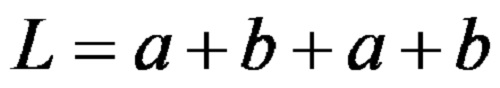
Истата формула запишана со помош на множители во пократка форма, гласи:
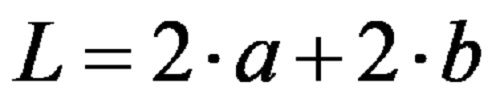
Пример број 1. Пресметај го периметарот на делтоид ако должината на неговата подолга страна е 15cm, а должината на неговата пократка страна е 11cm.
За да се реши задачата од пример број еден доволно е да:
a) Да се пресмета збирот од должините на сите четири страна. Собироците се: на две места подолгата страна и на две места пократката страна: L=15cm+11cm+15cm+11cm
б) Да се пресмета збир од две различни удвојувања на вредностите од подолгата и пократката страна на делтоидот.
Периметарот на делтоидот изнесува 52 центиметри!
Плоштина на делтоид
Плоштината на делтоид може да се пресмета со користење на хероновата формула како и кај било кој друг трапезоид (види пример решена задача со притискање на линкот). Единствената разлика е таа што плоштината кај оваа 2Д фигура со херонова формула кај кој е позната подолгата дијагонала пресметката е полесна затоа што во таа ситуација делтоидот е составен од два идентични триаголници.
Покрај стандардниот метод на решавање, плоштина на делтоид може да се пресмета со користење на формулата:
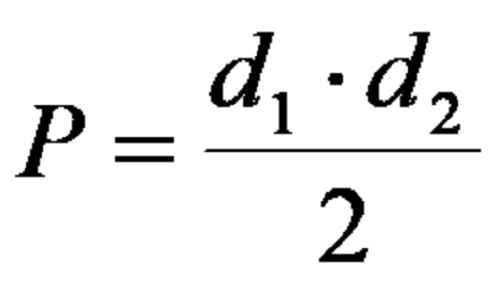
Секако, за да се користи формулата директно, треба да е позната должината на двете дијагонали на делтоидот. Доколку нивната должина е позната, плоштината може лесно да се одреди.
Пример број 2: Пресметај ја плоштината на делтоид ако се познати должините на неговите дијагонали кои изнесуваат 3cm и 16 cm.
За да се одреди плоштината доволно е:
- Да се одреди производот на дијагоналите.
- Производот на дијагоналите да се подели со 2.
Плоштината на делтоидот од примерот број два изнесува 24 центиметри квадратни.
Дијагоналите на делтоидот секогаш имаат различна должина. Тие се сечат меѓусебно под прав агол (агол од 90 степени). Делтоидот има една оска на симетрија.
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.


 Ве молиме почекајте ...
Ве молиме почекајте ...

