Како може да се изврши упростување на дропки пред множење? На оваа страница ќе видите на кој начин се упростуваат дропки пред да ги помножиме, со што ја избегнуваме постапката за нивно упростување по добивањето на конечниот производ. Овој метод е полесен затоа што во моментот пред множењето е полесно да се воочи со кој конкретен број може да се упростува, затоа што тука броевите со кои работиме се уште релативно помали.
Упростување дропки пред множење
При множење на две дропки, може да се врши упростување на следниов начин:
Ги лоцираме броевите кои при поставеност на дропките за множење градат замислена “дијагонала”. Такви две дијагонали градат:
- Броителот од првата дропка и именителот од втората дропка
- Именителот од првата дропка и именителот од втората дропка
Подолу, на сликата со различни бои се означени двете различни замислени дијагонали!
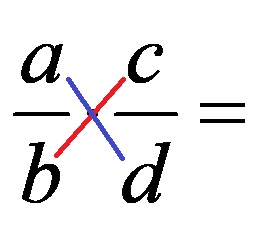
Ако броевите кои градат дијагонала имаат најголем заеднички делител кој е различен од 1, тогаш и двата броеви ги делиме со нивниот НЗД и количникот го запишуваме на нивното место. Притоа на овој начин може да упростуваме само по една или и по двете дијагонали!
Подолу, може да видите примери во кои упростувањето се врши пред да ги помножиме дропките една со друга!
Примери
Првиот пример подолу содржи упростување кое е можно само по една дијагонала, додека вториот пример може да се упростува и по двете дијагонали!
Пример 1: Упрости ги дропките што се дадени подолу пред да го извршиш множењето!
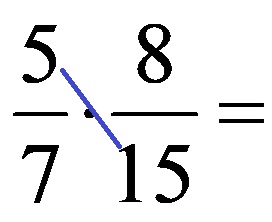
НЗД за броевите кои се наоѓаат во означената дијагонала (броевите 5 и 15) е бројот 5! Затоа и двата броеви ги делиме со бројот 5. Упростувањето треба да изгледа вака:
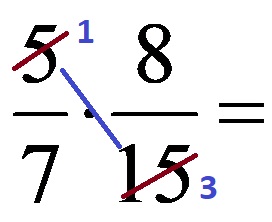
Ако последниот израз го запишеме без коригирани броеви, тој изгледа вака:
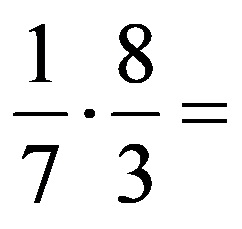
На крај, останува да ги помножиме дропките, со што се добива следниов конечен резултат:
Пример 2: Поедностави ги дропките пред да ги помножиш!
НЗД за броевите кои се наоѓаат во сината дијагонала (броевите 4 и 10) е бројот 2! Затоа и двата броеви ги делиме со бројот 2. Од друга страна НЗД за броевите кои се наоѓаат во црвената дијагонала (броевите 9 и 3) е бројот 3. Двата броеви од црвената дијагонала ги делиме со бројот 3! По упростувањето се добива следниов израз:
Ако последниот израз го запишеме без коригирани броеви, тој изгледа вака:
На крај, останува да ги помножиме дропките, со што се добива следниов конечен резултат:
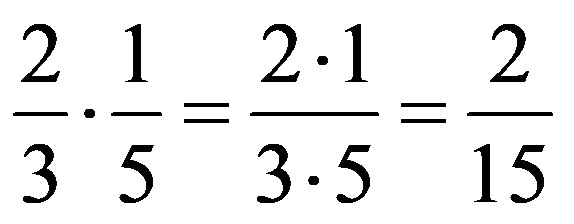
Видео примери
Во видеото подолу може да видите многу примери при кои се врши упростување на дропки пред да се помножат една со друга!
Доколку при множење на дропки една со друга, одлучите да не практикувате нивно упростување пред да ги помножите, тогаш на крај (кога ќе го добиете нивниот производ), мора да извршите упростување на финалниот резултат кој најверојатно ќе биде во форма на дропка!
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.
Tags: Дропки, Множење, Пред, Упростување



 Ве молиме почекајте ...
Ве молиме почекајте ...

