Разложување на прости множители е постапка при која одреден сложен број се претставува како производ од множители кои што се прости броеви! Во текстот знакот за множење е заменет со знакот x за полесно пишување и читање!
За потсетување:
- Прост број е број кој е делив со себеси и со бројот 1. При делење на прост број со било кој друг број (различен од 1 и од самиот број) се добива остаток.
- Сложен број е секој број кој покрај деливоста со себеси и бројот 1, е делив барем со уште еден број.
Податоци за разложување на прости множители
Подолу може да видите три различни примери за разложување на прости множители со решение и објаснување. Под овие три примери на располагање имате табела во која е претставено разложувањето на прости множители за броевите од 1 до 100. Во табелата како податоци може да се видат сите прости броеви кои постојат во дијапазон на броеви од 1 до 100. На дното на страницата ви се достапни разложувањата на сите броеви од 1 до 100 во видео!
Примери за разложување на прости множители
Пример 1: Разложи го бројот 14 на прости множители!
Бројот 14 може да го претставиме како производ од броевите 2 и 7. Затоа што и бројот 2 и бројот 7 се прости броеви, тука разложувањето завршува веднаш по реализирањето на првиот чекор! На цртеж, решението може да го претставиме на овој начин:
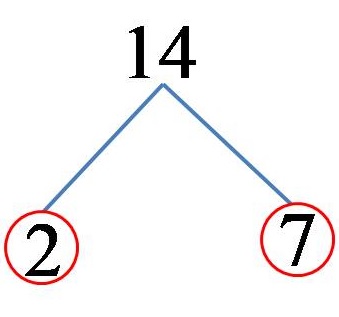
Од каде што следува дека бројот 14 разложен на неговите прости множители изгледа вака:
14 = 2 x 7
Пример 2: Разложи го бројот 30 на прости множители!
Бројот 30 може да го претставиме како производ од броевите 2 и 15. Затоа што и бројот 2 е прост број, веќе сме добиле еден прост множител за бројот 30. Од друга страна бројот 15 може да го претставиме како производ од броевите 3 и 5. Броевите 3 и 5 (и двата) се прости броеви, по што заклучуваме дека прости множители на бројот 30 се броевите 2,3 и 5.На цртеж, решението може да го претставиме на овој начин:
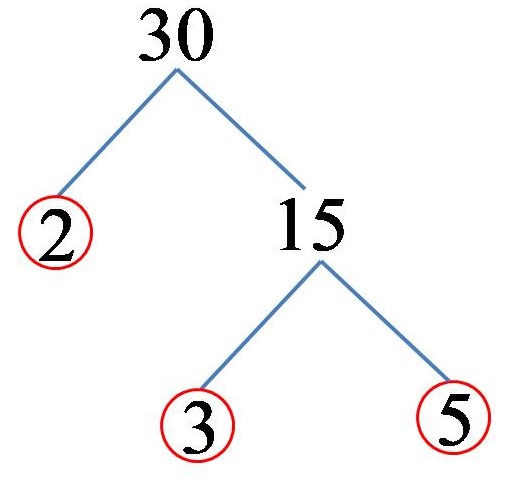
Од каде што следува дека бројот 30 разложен на неговите прости множители изгледа вака:
30 = 2 x 3 x 5
Пример 3: Разложи го бројот 42 на прости множители!
Бројот 42 може да го претставиме како производ од броевите 2 и 21. Бројот 2 е еден од простите множители на бројот 42! Од друга страна бројот 21 може да го претставиме како производ од броевите 3 и 7. Броевите 3 и 7 (и двата) се прости броеви, по што заклучуваме дека прости множители на бројот 42 се броевите 2,3 и 7.На цртеж, решението може да го претставиме на овој начин:
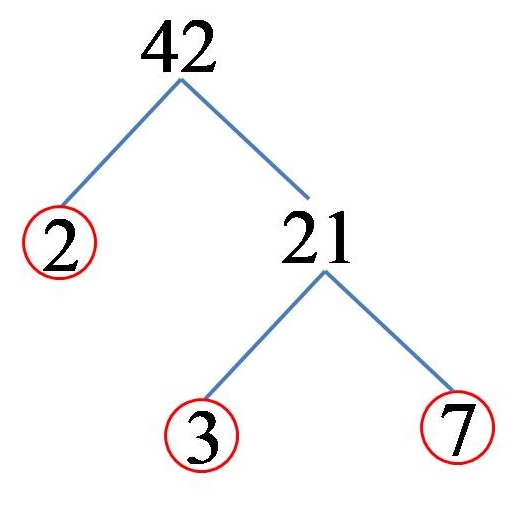
Од каде што следува дека бројот 42 разложен на неговите прости множители изгледа вака:
42 = 2 x 3 x 7
Табела за разложување
Табелата подолу соджи информации за разложувањето на прости множители за сите броеви од 1 до 100, како и податоци за сите прости броеви кои постојат од 1 до 100!
| Број | Разложување (ако е можно) |
|---|---|
| 1 | Прост број |
| 2 | Прост број |
| 3 | Прост број |
| 4 | 4 = 2 x 2 |
| 5 | Прост број |
| 6 | 6 = 2 x 3 |
| 7 | Прост број |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Прост број |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Прост број |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Прост број |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Прост број |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Прост број |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Прост број |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Прост број |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Прост број |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Прост број |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Прост број |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Прост број |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Прост број |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Прост број |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Прост број |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Прост број |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Прост број |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Прост број |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Прост број |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Прост број |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Прост број |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Прост број |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Прост број |
Видео примери
Видео материјалите содржат решение чекор по чекор за разложувањето на прости множители за сите броеви од 1 до 100:
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.
Tags: Множители, Прост, Прости, Разложување, Сложен



 Ве молиме почекајте ...
Ве молиме почекајте ...

