Питагорова теорема е една од најпознатите теореми во математика. Оваа теорема се применува во многу различни делови од математика и многу различни геометриски задачи. Питегоровата теорема важи само за правоаголен триаголник. Дефиниција на питагорова теорема: Кај правоаголен триаголник квадратот формиран над хипотенузата има еднаква плоштина со збирот од плоштините од квадратите над неговите катети.
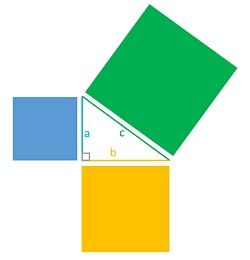
Хипотенуза е најдолгата страна во правоаголниот триаголник и истата секогаш се наоѓа наспроти правиот агол. Хипотенузата секогаш се означува со буквата c (це малечко латиница). Останатите две страни на правоаголниот триаголник, кои го формираат правиот агол се викаат катети. Катетите во правоаголниот триаголник се означуваат со буквите a и b (а и бе малечки латиница).
Формула за питагорова теорема
Формулата која ја претставува самата питагорова теорема, гласи:
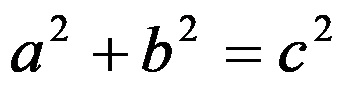
Логично, ако се познати двете катети на правоаголен триаголник, тогаш директно може да се одреди должината на неговата хипотенуза.
Пример број 1: Правоаголен триаголник има катети со должина 9cm и 40cm. Одреди ја должината на неговата хипотенуза!
Со замена на дадените вредности за катетите во главната формула се добива изразот:
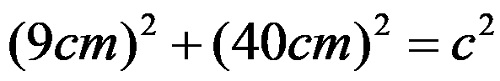
од каде по степенувањето се добива:
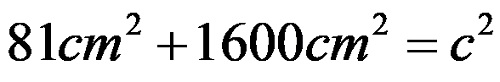
По формирањето на збирот се добива дека:
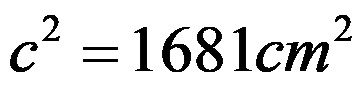
Со последниот израз се знае колку изнесува квадратот од должината на хипотенузата. За да се одреди должината на хипотенузата, целиот израз го коренуваме:
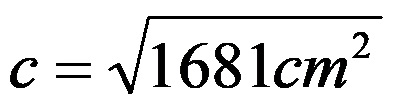
По пресметката на коренот десно од знакот за еднаквост, за должината на хипотенузата се добива вредноста 41cm.
Ако во одредена задача е позната една од катетите и хипотенузата, тогаш непознатата катета може да се одреди со помош на една од формулите:

Употребата на точната формула (од двете обоени формули погоре) зависи само од тоа која од катетите е дадена во конкретниот случај, а која е непознатата.
Пример број 2: Правоаголен триаголник има хипотенуза со должина 25cm. Една негова катета има должина 24cm. Одреди ја должината на непознатата катета!
По договор земаме дека познатата катета ќе ја означуваме со буквата a, а непознатата катета со буквата b. Во оваа ситуација ја користиме жолтата формула. Со замена на дадените вредности во неа, се добива изразот:
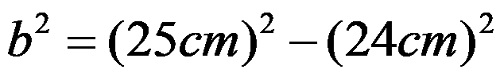
од каде по степенувањето се добива дека:
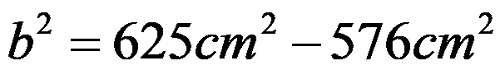
По одредувањето на разликата се добива:
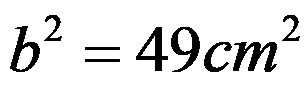
Од последниот израз се знае колку изнесува квадратот од должината на непознатата катета. За да се одреди нејзината должина, целиот израз го коренуваме:
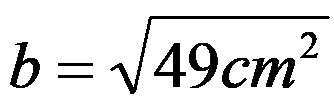
На крај, по коренувањето, лесно е да се одреди дека должината на непознатата катета изнесува 7cm.
Примена
Видеото подолу содржи визуализиран доказ за точноста на питагоровата теорема. Освен тоа во него може да видите повеќе примери за решени задачи.
Питагоровата теорема се користи секогаш кога со неа директно може да се одреди должина на непозната хипотенуза или катета кај правоаголен триаголник. Секако, во математика, правоаголен триаголник може да се сретне како дел од геометриско тело, замислен простор, дел од градба итн. На сите тие места каде што може да се утврди постоење на правоаголен триаголник, може и да се употребува питагорова теорема.
Употребата на оваа теорема е посебно важна во делот од математика – тригонометрија.
Доколку за даден правоаголен триаголник (како правоаголните триаголници од решените задачи погоре) се добива дека должините на неговите страни се цели броеви, тогаш за таквите три броеви се нарекуваат питагорови тројки. Од првиот решен пример, може да се заклучи дека броевите 9, 40 и 41 се питагорова тројка. Од вториот решен пример, може истото да се заклучи за броевите 7,24 и 25.
Видето претставено погоре содржи листа од неколку питагорови тројки.
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.
Tags: Задачи, Катети, Квадрат, Питагорова, Правоаголен, Теорема, Формула, Хипотенуза



 Ве молиме почекајте ...
Ве молиме почекајте ...

