Ромбоид е четириаголник кој има:
- Две по две паралелни спротивни страни
- Две по две еднакви спротивни страни
- Два по два еднакви спротивни агли
Ромбоидот се разликува со ромбот поради должината на страните, додека според големината на аглите се разликува со правоаголникот.
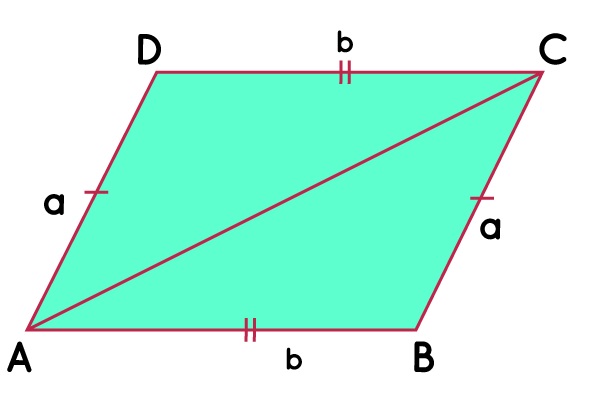
Периметар
Формулата за пресметување на периметар на робоид гласи:
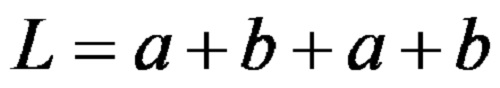
Истата формула запишана со помош на множители во пократка форма, гласи:
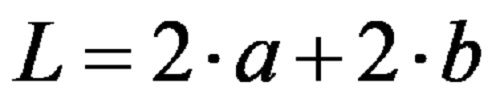
Пример број еден: Одреди го периметарот на ромбоид ако должината на неговата подолга страна е 10cm, а должината на неговата пократка страна е 7cm.
За да се реши задачата од пример број еден доволно е да:
a) Да се пресмета збирот од должините на сите четири страна. Собироците се: на две места подолгата страна и на две места пократката страна: L=10cm+7cm+10cm+7cm
б) Да се пресмета збир од две различни удвојувања на вредностите од подолгата и пократката страна на ромбоидот.
Периметарот на ромбоидот изнесува 16 центиметри!
Плоштина на ромбоид
Формулата за пресметување на плоштина на ромбоид гласи:

Плоштина на ромбоид може да се пресмета како производ од една од страните на ромбоидот и висината која и е соодветна.
Пример број два: Пресметај ја плоштината на ромбоид со страна 7cm, ако должината на неговата висина (соодветна за дадената страна) изнесува 5cm.
При пресметката доволно е да помножиме 7cm со 5cm.
Плоштината на ромбоидот од примерот број два изнесува 35 центиметри квадратни.
Формулите за пресметување на периметар и плоштина на ромбоид се составен дел од задачи во кои треба да се пресмета периметар и плоштина на сложени фигури. Исто така формулите се користат како дел од задача за пресметување на плоштина на одредени геометриски тела кои имаат страна или повеќе страни кои ја имаат формата ромбоид.
Ромбоидот има две дијагонали кои немаат еднаква должина. Двете дијагонали се сечат точно на половина и образуваат два по два еднакви агли. Оваа геометриска фигура нема оска на симетрија.
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.


 Ве молиме почекајте ...
Ве молиме почекајте ...

